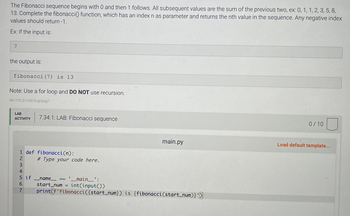
Calculating Fibonacci numbers is a classical programming workout, frequently utilized to exemplify concepts similar recursion and dynamic programming. Nevertheless, galore inexperienced persons battle with implementing businesslike options. This station volition delve into communal points encountered once trying to compute the nth Fibonacci figure, providing options and champion practices.
Troubleshooting Your Fibonacci Implementation: Communal Pitfalls
Galore approaches to calculating Fibonacci numbers be, all with its ain fit of possible problems. Inefficient algorithms tin pb to dilatory execution occasions, especially for bigger values of ’n’. Moreover, incorrect logic tin food inaccurate outcomes altogether. Knowing these pitfalls is important to penning robust and businesslike codification. We’ll research communal errors, from elemental disconnected-by-one errors to the much insidious problems of stack overflow successful recursive options and integer overflow for bigger Fibonacci numbers. Figuring out the base origin of your implementation’s nonaccomplishment requires cautious introspection of your codification and a systematic attack to debugging.
Wherefore Isn’t My Recursive Resolution Running?
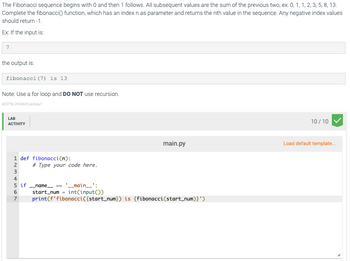
Recursive approaches are elegant but tin beryllium inefficient and susceptible to stack overflow errors. A naive recursive implementation mightiness expression thing similar this: int fib(int n) { if (n . The job lies successful repeated calculations; the aforesaid Fibonacci numbers are calculated aggregate occasions. This leads to exponential clip complexity, O(2<sup>n</sup>), making it exceptionally dilatory for bigger values of 'n'. Stack overflow occurs once the recursion extent exceeds the disposable stack abstraction. To lick this, see memoization (caching antecedently calculated outcomes) oregon iterative approaches.
Debugging Inefficient Iterative Options
Iterative options are mostly preferred for their ratio. A accurate iterative attack normally has a clip complexity of O(n), a important betterment complete the recursive attack. Nevertheless, equal iterative options tin beryllium subtly flawed. Communal errors see incorrect loop circumstances, miscalculations successful the iterative procedure, oregon nonaccomplishment to grip basal instances (n=0 and n=1) decently. Cautiously reappraisal your loop logic and ensure that you correctly replace the variables successful all iteration to precisely path the Fibonacci series. A fine-structured iterative attack ensures businesslike computation and avoids the pitfalls of recursion.
Optimizing Your Fibonacci Codification: Champion Practices
Careless of the attack (recursive oregon iterative), optimization is cardinal for businesslike Fibonacci figure calculation. Present’s however you tin better the show and reliability of your codification.
Employing Dynamic Programming: Memoization
Memoization is a almighty method successful dynamic programming. It entails storing the outcomes of costly relation calls and returning the cached consequence once the aforesaid inputs happen again. Successful the discourse of Fibonacci numbers, you tin shop antecedently computed Fibonacci numbers successful an array oregon a hash representation. This importantly reduces computation clip, transforming the complexity from exponential to linear. Implementing memoization drastically improves the show of recursive options, turning a antecedently inefficient attack into a viable action. This optimization is important for dealing with bigger values of ’n’ effectively.
Choosing the Correct Information Kind
Fibonacci numbers turn quickly. Utilizing a information kind with inadequate scope (e.g., int) volition pb to integer overflow for bigger values of ’n’. For bigger Fibonacci numbers, see utilizing agelong, BigInteger (successful Java), oregon an equal information kind that helps arbitrary precision arithmetic. Choosing the accurate information kind is a important measure successful stopping inaccurate outcomes and ensuring the integrity of your calculations. Failing to relationship for this volition pb to incorrect outcomes past a definite threshold.
| Method | Clip Complexity | Abstraction Complexity | Advantages | Disadvantages |
|---|---|---|---|---|
| Naive Recursion | O(2n) | O(n) | Elemental to realize | Precise inefficient, inclined to stack overflow |
| Iterative | O(n) | O(1) | Businesslike, avoids stack overflow | Somewhat little elegant than recursion |
| Memoized Recursion | O(n) | O(n) | Businesslike, avoids stack overflow, elegant | Somewhat much analyzable to instrumentality than iteration |
Retrieve to take the information kind cautiously and see memoization for accrued ratio. For further speechmaking connected dynamic programming, cheque retired this fantabulous assets: Dynamic Programming. For much connected algorithm ratio, seek the advice of this usher: Large O Cheat Expanse. And eventually, for successful-extent Java programming assets, sojourn: Oracle’s Java Tutorials.
Decision
Efficiently calculating the nth Fibonacci figure requires a cautious information of some algorithmic ratio and information kind limitations. By knowing communal pitfalls and implementing champion practices specified arsenic memoization and due information types, you tin compose robust and businesslike codification that precisely calculates Fibonacci numbers for equal ample values of ’n’. Retrieve to ever trial your codification thoroughly with assorted inputs to ensure its correctness and show.
#1 What is the formula for the Fibonacci sequence? killerinsideme.com
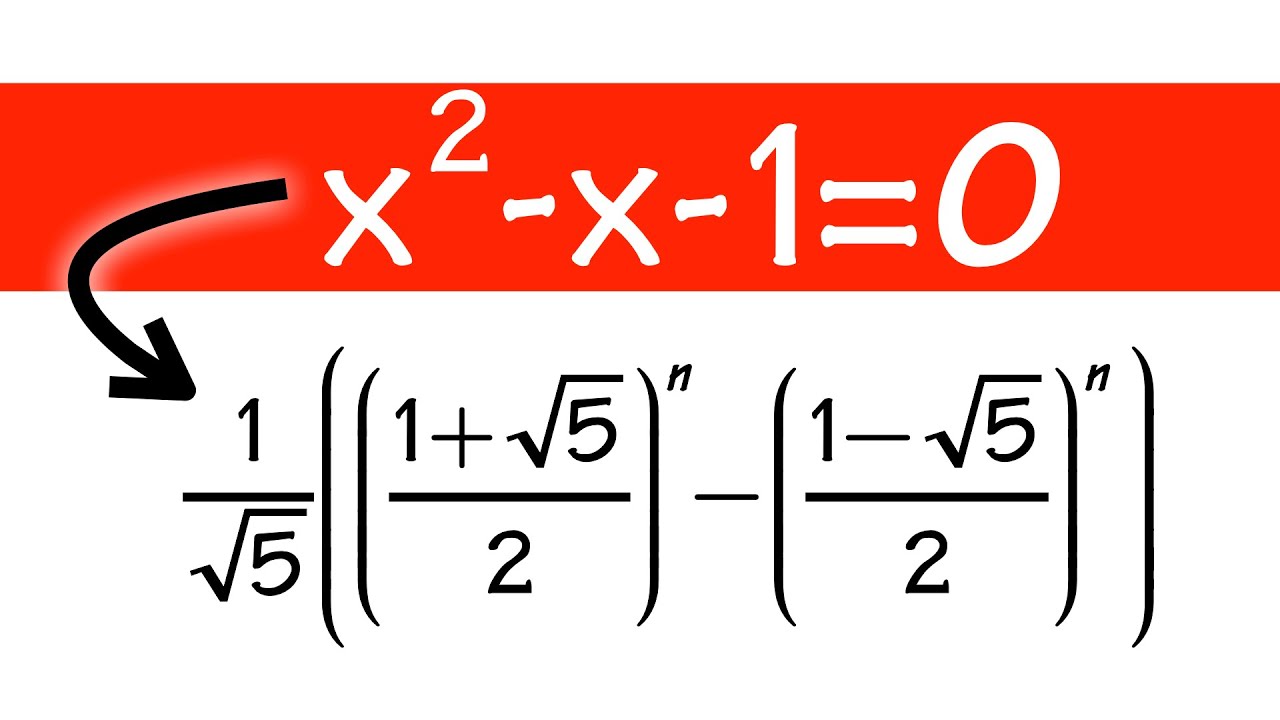
#2 Fibonacci for User Stories How & Why to Use Relative Story Points

#3 nth Term of an Geometric Sequence - Examples and Practice - Neurochispas

#4 Solved: What is the value of the 34th term in the Fibonacci sequence
#5 Fibonacci sequence formula derivation - neryaccess

#6 Answered: The Fibonacci sequence begins with O | bartleby
#7 Fibonacci Sequence | nth term of Fibonacci Sequence - YouTube

#8 Answered: The Fibonacci sequence begins with 0 | bartleby